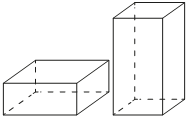
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
Объем прямоугольной призмы:
V=S*h, где S - площадь основания, h - высота призмы, которая совпадает с ребром призмы.
В основании правильной призмы лежит правильный многоугольник, в данном случае
квадрат, следовательно площадь основания такой призмы:
S=a2, где a - сторона
квадрата.
Тогда:
V1=a12h1 - объем первой коробки.
V2=a22h2 - объем второй коробки.
Из условия известно, что:
4,5h1=h2
a1=3a2
Найдем отношение объемов:
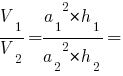
Подставляем равенства из условия:
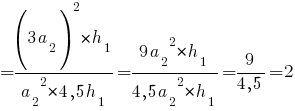
Т.е. первая коробка по объему в два раза больше второй.
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
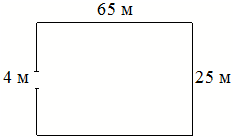Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
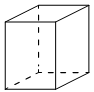Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
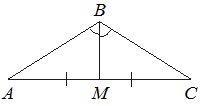В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
Какой наименьший угол (в градусах) образуют минутная
и часовая стрелки часов в 17:00?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: