
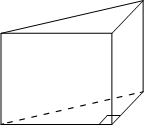
 В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
Объем прямой призмы равен произведению площади основания и высоты.
Высота известна, найдем площадь основания.
Площадь прямоугольного треугольника равна половине произведения катетов.
По теореме Пифагора найдем второй катет (обозначим его длину как x):
(√
34=9+x2
x2=34-9=25
x=5
Sоснования=3*5/2=15/2=7,5
V=7,5*6=45
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
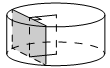 Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
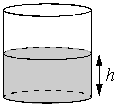 Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
 Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
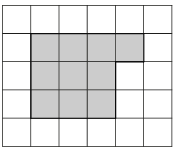 План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
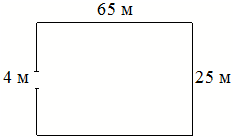 Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.

Комментарии: