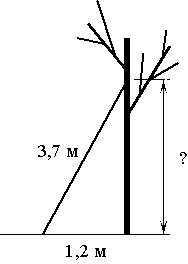
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Земля, ствол дерева и лестница представляют из себя
прямоугольный треугольник, где лестница - гипотенуза, а ствол и земля - катеты.
Обозначим высоту, на которой находится конец лестницы, как Х.
По
теореме Пифагора:
3,72=1,22+X2
13,69=1,44+X2
X2=13,69-1,44
X2=12,25
X=3,5
Ответ: 3,5
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.
Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
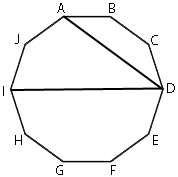ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-12-18 13:21:41) Полина : здравствуйте я не поняла со строки ответа как вы из 12,25 получили 3,5 ?
(2017-06-03 19:38:48) Администратор: Аня, с какой строки Вы не поняли?
(2017-06-02 17:10:11) аня: я не поняла