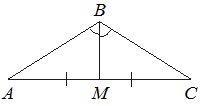
В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
Так как медиана делит угол пополам, то она так же является и
биссектрисой. Одновременно быть и
биссектрисой и медианой отрезок может только в равнобедренном треугольнике (по
свойству равнобедренного треугольника), тогда этот отрезок так же является и
высотой.
Т.е. треугольник ABM - прямоугольный.
∠ABM=∠B/2=120°/2=60°
Так как ABM прямоугольный, то по определению косинуса:
cos∠ABM=BM/AB
cos60°=27/AB (cos60°=1/2 по таблице)
1/2=27/AB |*2
1=54/AB
AB=54
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
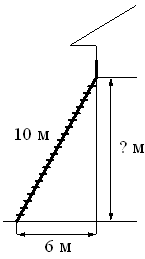Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
В параллелограмме ABCD диагонали делят его углы пополам и равны 40 и 42. Найдите периметр параллелограмма ABCD.
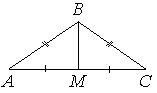В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
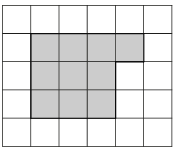План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
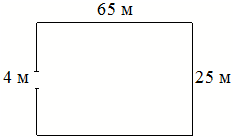Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: