В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Проведем высоты как показано на рисунке. И рассмотрим треугольник CDF. Это
прямоугольный треугольник (т.к. /CFD - прямой).
По
теореме о сумме углов треугольника найдем угол FCD
/FCD=180°-90°-45°=45°. Заметим, что /FCD=/FDC. Следовательно, треугольник
равнобедренный (по
свойству равнобедренного треугольника). Отсюда следует, что FD=FC (по
определению равнобедренного треугольника).
Рассмотрим треугольник ABE. /BAE=/FDC=45° (т.к. по условию задачи
трапеция равнобедренная).
Аналогично по
теореме о сумме углов треугольника получим, что /ABE=180°-90°-45°=45°, а следовательно (аналогично предыдущему треугольнику) треугольник ABE -
равнобедренный.
Причем эти треугольники равны (AB=CD, BE=CF и /ABE=/FCD -
первый признак равенства)=> AE=FD.
Рассмотрим четырехугольник BCFE.
Т.к. BC||EF, BE и FC - высоты, следовательно /BEF=90°=/CFE. /EBC=/BCF=90°. Следовательно четырехугольник BCFE -
прямоугольник => BC=EF.
Теперь можем записать:
AD=AE+EF+FD, 8=AE+2+FD, 8=AE+2+AE
6=2*AE => AE=3.
Т.к. AE=BE=3, а BE-высота трапеции, то теперь можем вычислить
площадь трапеции.
Sтрапеции=(BC+AD)/2*BE
Sтрапеции=(2+8)/2*3=15.
Ответ: Sтрапеции=15.
Поделитесь решением
Присоединяйтесь к нам...
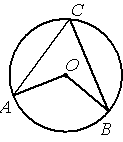Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Укажите номера верных утверждений.
1) Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая медиана равнобедренного треугольника является его биссектрисой.
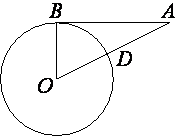Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-12 14:12:34) Администратор: Раньше мы доказали что треугольники ABE и DCF равны, поэтому FD=AE. Цитата из решения "Причем эти треугольники равны (AB=CD, BE=CF и /ABE=/FCD - первый признак равенства)=> AE=FD."
(2015-04-12 14:03:16) : непонятно , почему там fd ПРЕВРАТИЛОСЬ В AE?Теперь можем записать: AD=AE+EF+FD, 8=AE+2+FD, 8=AE+2+AE