
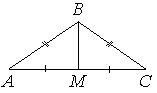
 В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
Треугольник ABC -
равнобедренный (по условию).
Тогда, по третьему свойству равнобедренного треугольника, BM является высотой.
Т.е. треугольник ABM - прямоугольный.
AM=AC/2=24/2=12 (так как BM -
медиана).
По теореме Пифагора:
AB2=BM2+AM2
152=BM2+122
225=BM2+144
BM2=81
BM=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
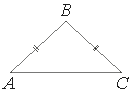 В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
 В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
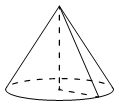 Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.
Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.
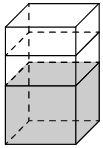 В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.


Комментарии: