
 Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
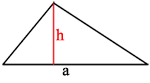
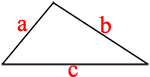
Площадь боковой поверхности пирамиды равна сумме боковых граней пирамиды, которые являются равными треугольниками со сторонами 16, 17 и 17.
Площадь такого треугольника легче вычислить через три стороны (формула Герона).
Полупериметр:
p=(16+17+17)/2=50/2=25
S=√p(p-a)(p-b)(p-c)=√25(25-16)(25-17)(25-17)=√25*9*8*8=
По свойству арифметического корня:
=√25*√9*√8*8=5*3*8=120
Это площадь одной боковой грани, значит площадь всей боковой поверхности:
Sбп=3*S=3*120=360
Ответ: 360
Поделитесь решением
Присоединяйтесь к нам...
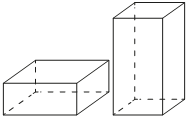 Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
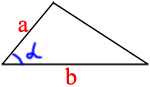
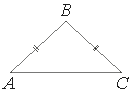 В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
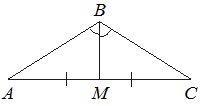 В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
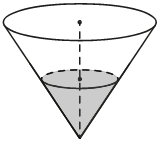 В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.


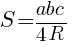
Комментарии: