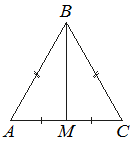В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
По
третьему свойству равнобедренного треугольника, BM является не только медианой, но и
высотой.
Следовательно, треугольник ABM -
прямоугольный.
Тогда tgA=BM/AM (по определению tg).
А так как по условию thA=12/5, то:
BM/AM=12/5
12/AM=12/5 |:12
1/AM=1/5
AM=5
AM и BM - катеты треугольника ABM. Необходимо найти AB. Воспользуемся
теоремой Пифагора:
AB2=AM2+BM2
AB2=52+122
AB2=25+144=169
AB=√169=13
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
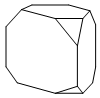От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
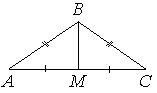В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 145°, угол ABC равен 113°. Найдите угол ACB. Ответ дайте в градусах.
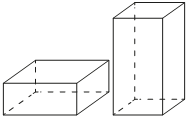Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
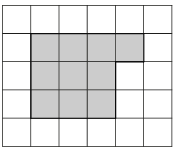План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: