Постройте график функции y=|x|(x+1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x(x+1)-6x, при x≥0
y=(-x)(x+1)-6x, при x<0
y=x2+x-6x, при x≥0
y=-x2-x-6x, при x<0
y=x2-5x, при x≥0
y=-x2-7x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
1) y=x2-5x, при x≥0
Графиком данной подфункции является парабола. Ветви этой параболы направлены вверх, так как коэффициент при x2 положительный.
Найдем корни уравнения x2-5x=0
x(x-5)=0
x1=0
x-5=0
x2=5
Построим график по точкам:
| X | 0 | 1 | 5 | 6 |
| Y | 0 | -4 | 0 | 6 |
| X | 0 | -1 | -7 | -8 |
| Y | 0 | 6 | 0 | -8 |
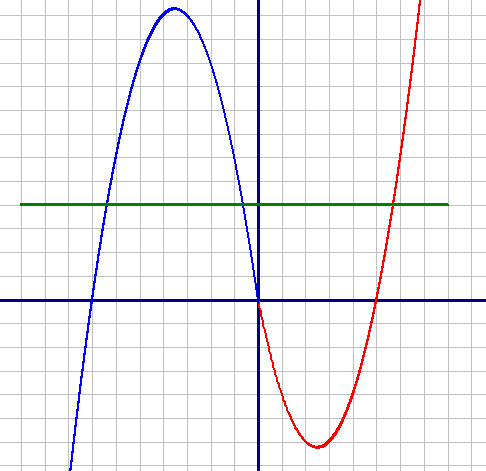Красный график: y=x2-5x, при x≥0Поделитесь решением
Присоединяйтесь к нам...
Упростите выражение
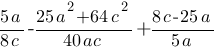и найдите его значение при a=87, c=51. В ответе запишите найденное значение.
Автобус проехал x километров и израсходовал при этом 27 литров топлива. На сколько километров хватит 80 литров топлива при таких же условиях езды? Запишите соответствующее выражение.
Мотоцикл проехал x километров и израсходовал при этом 17 литров бензина. На сколько километров хватит 40 литров бензина при таких же условиях езды? Запишите соответствующее выражение.
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле T=2√
Решите уравнение x2-6x+√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: