
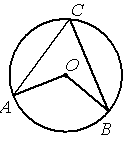
 Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=110°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 110°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 110/2=55.
Ответ: /ACB=55°.
Поделитесь решением
Присоединяйтесь к нам...
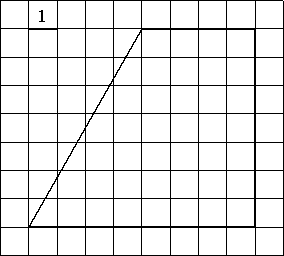 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
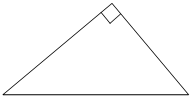 Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
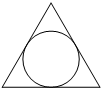 Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
3) Площадь круга меньше квадрата длины его диаметра.
Комментарии: