
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
Рассмотрим каждое утверждение.
1) "Вокруг любого треугольника можно описать окружность", это утверждение верно (по
теореме об окружности)
2) "Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны". Это утверждение верно (по
свойству углов).
3) "Площадь треугольника не превышает произведения двух его сторон." Площадь треугольник можно вычислить по формуле Sтреугольника=1/2*a*b*sinC, где С - угол между сторонами a и b. Т.к. значение синуса не может быть больше единицы, получается, что a*b всегда больше 1/2*a*b*sinC. Поэтому это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
 В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
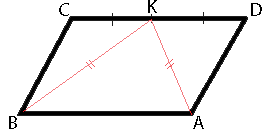 В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
Комментарии: