
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны", это утверждение верно (по
признаку параллельности прямых)
2) "Диагональ
трапеции делит её на два равных треугольника." Во-первых, нет такого
свойства трапеции. 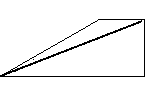 Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
3) "Если в
ромбе один из углов равен
90°, то такой ромб — квадрат". Чтобы ромб был квадратом, необходимо, чтобы все 4 угла были равны 90°.
Т.к.
ромб - частный случай
параллелограмма, то к нему и применимы все
свойства параллелограмма, следовательно (по
свойству параллелограмма), противоположный прямому углу, угол тоже равен 90°.
Другие два угла по тому же свойству равны друг другу.
Сумма углов многоугольника вычисляется по формуле (n-2)*180°, где n - количество углов. В нашем случае, углов - 4. Тогда сумма углов равна (4-2)*180°=360°.
Тогда получается, что сумма двух неизвестных углов равна 360°-90°-90°=180°. А так как они равны друг другу, то каждый из них равен 180°/2=90°.
Т.е. мы узнали, что все четыре угла равны по 90°, следовательно это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
 Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
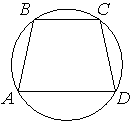 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
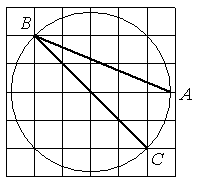 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Комментарии:
(2015-04-11 12:09:16) Администратор: Света, спасибо за уточнение, исправлено.
(2015-04-11 00:21:53) света: по 1)-это признак параллельности прямых ,а не свойство