Парабола проходит через точки K(0;-5), L(3;10), M(-3;-2). Найдите координаты её вершины.
Парабола - это график квадратичной функции ƒ(x)=ax2+bx+c.
Если парабола проходит через некую точку (H;K), то верно, что K=aH2+bH+c.
Следовательно, мы можем записать:
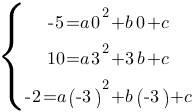
Вычтем из второго уравнения третье:
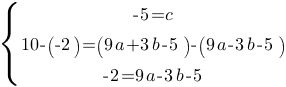
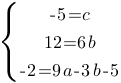
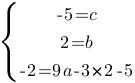
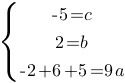
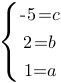
Т.е. получаем функцию:
ƒ(x)=x2+2x-5
Координату "х" вершины параболы найдем по формуле:
x0=-b/(2a)=-2/(2*1)=-1
y0(x0)=(-1)2+2(-1)-5=1-2-5=-6
Ответ: (-1;-6)
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения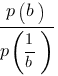 
, если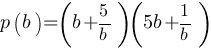 
В какое из следующих выражений можно преобразовать дробь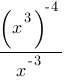 
?
1) x-9
2) x-15
3) x4
4) x2
Уравнение x2+px+q=0 имеет корни -5 и 2. Найдите q.
Найдите значение выражения (1,8*10-3)(7*10-2).
Постройте график функции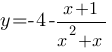 
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: