Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
Рассмотрим каждое утверждение.
1) "Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности", это утверждение неверно,т.к. все зависит от расположения окружностей. Например, если центры окружностей совпадают, то окружности не пересекутся.
2) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны", это утверждение верно (по
свойству углов)
3) "У
равнобедренного треугольника есть
центр симметрии", это утверждение неверно, т.к. у
равнобедренного треугольника есть только
осевая симметрия (ось совпадает с медианой опущенной к основанию).
Поделитесь решением
Присоединяйтесь к нам...
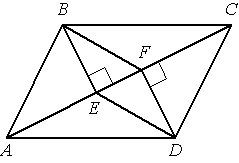В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
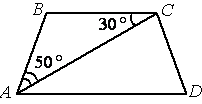Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: