
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.
Рассмотрим каждое утверждение.
1) "Каждая из биссектрис равнобедренного треугольника является его высотой", это утверждение неверно, т.к. по
свойству равнобедренного треугольника, только биссектриса, проведенная к основанию является его высотой.
2) "Диагонали прямоугольника равны", это утверждение верно (по
свойству прямоугольника).
3) "У любой трапеции основания параллельны", это утверждение верно (по
определению трапеции).
Поделитесь решением
Присоединяйтесь к нам...
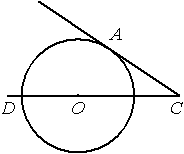 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
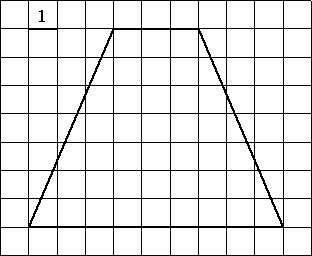 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
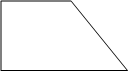 Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
 Площадь прямоугольного треугольника равна 8√
Площадь прямоугольного треугольника равна 8√
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Комментарии:
(2023-11-04 15:37:54) Ксения: Сторона ромба равна 7, а один из углов равен 150°. Найдите высоту