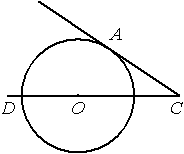
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
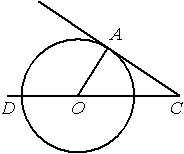Проведем отрезок ОА.
/DOA -
центральный угол для данной окружности. Он опирается на дугу AD, равную 140°. Следовательно, /DOA тоже равен 140°.
/AOC -
смежный углу DOA, поэтому /AOC=180°- /DOA=180°-140°=40°.
Треугольник ACO -
прямоугольный, т.к. радиус всегда перпендикулярен
касательной (по
свойству касательной). Т.е. /ОАС=90°. Применяя
теорему о сумме углов треугольника, можем записать:
180°=/AСO+/CAO+/AOC.
/AСO=180°-/CAO-/AOC=180°-90°-40°=50°.
Ответ: /ACO=50°.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, BC=5, AC=2.
Найдите tgB.
Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
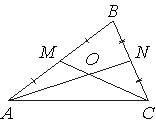Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=18. Найдите CO.
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: