Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.
Рассмотрим каждое утверждение.
1) "Каждая из биссектрис равнобедренного треугольника является его высотой", это утверждение неверно, т.к. по
свойству равнобедренного треугольника, только биссектриса, проведенная к основанию является его высотой.
2) "Диагонали прямоугольника равны", это утверждение верно (по
свойству прямоугольника).
3) "У любой трапеции основания параллельны", это утверждение верно (по
определению трапеции).
Поделитесь решением
Присоединяйтесь к нам...
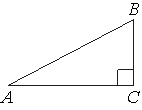В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
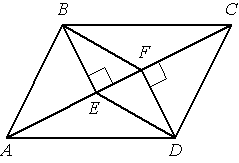В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-11-04 15:37:54) Ксения: Сторона ромба равна 7, а один из углов равен 150°. Найдите высоту