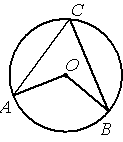
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=128°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 128°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 128/2=64.
Ответ: /ACB=64°.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 4, тангенс угла BAC равен 0,75. Найдите радиус вписанной окружности треугольника ABC.
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
У треугольника со сторонами 4 и 16 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: