
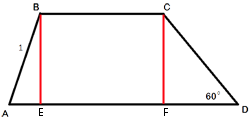
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
 Проведем
высоты BE и CF как показано на рисунке.
Проведем
высоты BE и CF как показано на рисунке.
Рассмотрим треугольник CDF. Он
прямоугольный, т.к. CF-высота.
По
теореме о сумме углов треугольника /FCD=180°-90°-60°=30°.
По
определению синуса sin/FCD=DF/CD=sin30°=1/2
Т.е. DF=CD/2, CD, в свою очередь, по условию задачи равно AD/2, получам, что DF=AD/4.
BC=AD/2 (по условию задачи)
EF=BC=AD/2 (т.к. BCFE - прямоугольник)
Вычислим AE, AE=AD-DF-EF=AD-AD/4-AD/2=AD/4, т.е. мы получили, что AE=FD
Рассмотрим треугольники ABE и DCF:
BE=CF (т.к. BCFE - прямоугольник)
AE=FD (только что получили)
/AEF=90°=/DFC, тогда по
первому признаку равенства, треугольники ABE и DCF равны.
Следовательно, AB=CD, т.е. наша
трапеция равнобедренная.
AB=CD=1 (по условию задачи), AD=2*CD=2*BC=2 (тоже по условию), BC=CD=1
FD=AD/4=0,5
По
теореме Пифагора CD2=CF2+FD2
12=CF2+0,52
CF2=0,75
CF=√
SABCD=(BC+AD)/2*CF=(1+2)/2*0,5√
SABCD=0,75√
Ответ: SABCD=0,75√
Поделитесь решением
Присоединяйтесь к нам...
 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
 В трапеции ABCD основания AD и BC равны соответственно 48 и 3, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.
В трапеции ABCD основания AD и BC равны соответственно 48 и 3, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.
 Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
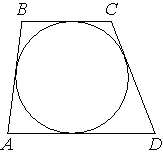 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Комментарии:
(2016-04-08 20:57:08) Администратор: Даниил, спасибо большое еще раз, исправлено!
(2016-04-08 20:54:33) Даниил: ошибка после того когда доказали угол /AEF=90°=/DFC ,тогда по первому признаку равенства, треугольники ABC и DCF равны. не ABC ,а ABE
(2016-04-08 20:34:49) Администратор: Даниил, спасибо за найденную опечатку. Исправлено!
(2016-04-08 20:29:21) Даниил: ошибка после того когда доказали AE=FD ,смотрим треугольники не ABC и DCF ,а ABE и DCF
(2015-05-20 16:36:40) Григорий: Спасибо, теперь всё понятно.
(2015-05-19 22:04:59) Администратор: Григорий, я уточнил решение, думаю, так будет понятней.
(2015-05-19 21:23:54) Григорий: откуда взялось 0,5корень из 3
(2015-05-19 21:23:54) Григорий: откуда взялось 0,5корень из 3
(2015-05-10 15:43:45) Администратор: Диана, к сожалению, у меня нет такой информации.
(2015-05-10 15:39:54) Диана: Это задача 1-ой части? или 2-ой части?