
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Рассмотрим каждое утверждение:
1) "Существует квадрат, который не является прямоугольником" - это утверждение неверно, т.к. противоречит определению квадрата.
2) "Если два угла треугольника равны, то равны и противолежащие им стороны", это утверждение верно по
свойству равнобедренного треугольника.
3) "Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.", это утверждение верно по
свойству углов.
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен √
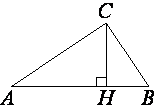 В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
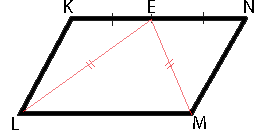 В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
 Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Комментарии: