
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Вариант №1 (Предложил пользователь Елена)
Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
К тому же, по условию задачи, точка Р - середина стороны BC, т.е. BM -
серединный перпендикуляр к стороне BC.
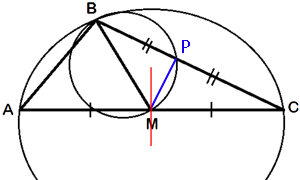 Проведем
серединный перпендикуляр к стороне AC, как показано на рисунке.
Проведем
серединный перпендикуляр к стороне AC, как показано на рисунке.
Центр
описанной окружности совпадает с точкой пересечения
серединных перпендикуляров треугольника, а в данном случае - это точка М, т.е. точка М и есть центр
описанной окружности.
Так как получилось, что центр окружности лежит на стороне описываемого треугольника, то AM и MC - радиусы данной окружности и равны R=AC/2=4/2=2.
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Укажите номера верных утверждений.
1) Диагонали любого прямоугольника равны.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
Комментарии:
(2017-01-17 23:52:32) Администратор: cdtbdn, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-17 10:34:25) cdtbdn : ответы решить задачу по геометрии на рисунке an паролейна bm и an = bm. докажите что треугольник and = треугольнику bmd с ответами и решением
(2016-02-14 18:05:00) Администратор: Виктория, почти все правильно, кроме последнего предложения. В условии не сказано, в первом решении мы это выяснили исходя из серединных перпендикуляров, а во втором решении мы выяснили, что треугольник ABC прямоугольный, а (по свойству описанной окружности) центр описанной вокруг прямоугольного треугольника лежит на середине гипотенузы, т.е. в точке М. Вот поэтому АМ=МС=ВМ=R=2.
(2016-02-11 18:55:41) Виктория: Правильное ли рассуждение у меня? Из т.М опустим перпендикуляр к т.Р. Отрезок МР делит ВС пополаам и перпендикулярен ему. Рассмотрим треугольники ВМР и МРС. Т.к. МР - общая сторона, углы ВРМ и МРС - прямые (равны), и по условию ВР=РС, след-но треугольники ВМР и МРС равны.Поэтому ВМ =МС. Т.к. окружность с центром в т.М явл-ся описанной вокруг треугольника АВС,тт.АВС лежат на окружности и равноудалены от т.М, то АМ=МС=ВМ=R=2
(2015-05-28 14:13:14) Анна: спасибо
(2015-05-08 21:55:32) Елена: Спасибо
(2015-05-03 22:53:26) Администратор: Елена, я добавил Ваш вариант решения на сайт. Спасибо за интересный подход.
(2015-04-10 02:43:36) Елена: Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров к сторонам треугольника. Доказали, что РМ серединный перпендикуляр к стороне ВС. Точка пересечения РМ и серединного перпендикуляра к стороне АС лежит на прямой, проходящей через точку М. А это и есть точка М. М - центр окружности, описанной около треугольника АВС, значит радиус равен 2.
(2014-05-28 13:47:33) Администратор: Ольга, да действительно, у меня уже "глаз замылился"...
(2014-05-28 11:27:59) Ольга: Так вроде это признак: равенство угла и пропорциональность сторон, к нему прилежащих (относятся как 1 к 2, т.к. М и Р середины). Впрочем я не настаиваю
(2014-05-28 10:29:20) Администратор: Ольга, к сожалению, в 9-ом классе далеко не все ученики могут думать даже на два шага вперед (я сужу по вопросам, какие они задают), поэтому доказывать подобие нужно только через признаки подобия. Ваше доказательство идет через определение подобия, причем двух-ходовое. Поэтому думаю, что большинству пользователей будет непонятно. Успехов Вашему ребенку на экзаменах!!!
(2014-05-28 09:45:50) Ольга: Насчет подобия мне кажется понять не трудно. Насчет учителя математики - нет, я - мама ученика, который собирается сдавать ГИА по математике. Так что приходится участвовать в процессе и вспоминать подзабытое
(2014-05-27 19:34:31) Администратор: Ольга, я понял Вашу мысль, но боюсь, что пользователям будет трудно понять это подобие, Вы так не думаете? А Вы случайно не учитель математики?
(2014-05-27 19:30:34) Ольга: Нет, всё-таки CPM
(2014-05-27 19:26:00) Ольга: Извините, ошиблась, вместо CPM - BPM
(2014-05-27 14:17:27) Ольга: После того как доказали, что треугольник СРМ - прямоугольный, надо написать что он подобен треугольнику АВС, по углу С - общий угол, и двум сторонам ( Р - середина ВС, М -середина АС), следовательно угол В - прямой