Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
AB=BC=CD=AD=DH+CH=21+8=29 (по
определению ромба).
Рассмотрим треугольник AHD.
AHD -
прямоугольный (т.к. AH -
высота), тогда по
теореме Пифагора: AD2=AH2+DH2
292=AH2+212
841=AH2+441
AH2=400
AH=20
Ответ: AH=20
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
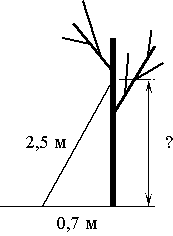Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-20 23:56:06) Администратор: Наталья, для этого и трудимся. Спасибо и Вам.
(2017-02-20 23:15:17) Наталья: Замечательный сайт, в геометрии не сильно шарю а в этом году огэ сдавать ваш сайт стал для меня находкой, очень подробно и понятно всё объясняется ❤
(2015-02-21 12:32:03) Администратор: Виктория, спасибо и Вам за теплые слова.
(2015-02-21 11:16:00) Виктория: Как замечательно, что существует этот сайт. Спасибо вам огромное)
(2014-12-12 20:31:53) Эбонит: норм
(2014-06-13 14:59:47) динара : спасибо