Укажите номера верных утверждений.
1) Диагонали любого прямоугольника равны.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
Рассмотрим каждое утверждение.
1) "Диагонали любого
прямоугольника равны" - это утверждение верно, т.к. является одним из
свойств прямоугольника.
2) "Если в треугольнике есть один острый угол, то этот треугольник остроугольный" - это утверждение неверно, т.к. не соответствует
определению остроугольного треугольника.
3) "Если точка лежит на
биссектрисе угла, то она равноудалена от сторон этого угла". Расстояние от точки до прямой - отрезок, проведенный из данной точки перпендикулярно прямой.
Рассмотрим рисунок.
Треугольники ABD и BCD -
прямоугольные, т.к. AD и DC - расстояние от точки D (расположенной на биссектрисе) до лучей угла. Сторона BD - общая для этих треугольников, /ABD=/CBD, по
определению биссектрисы. Следовательно,
синусы этих углов тоже равны.
По
определению синуса, sin(ABD)=sin(CBD)=AD/BD=CD/BD, следовательно AD=CD. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
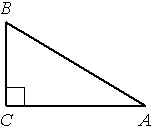В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
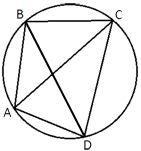Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
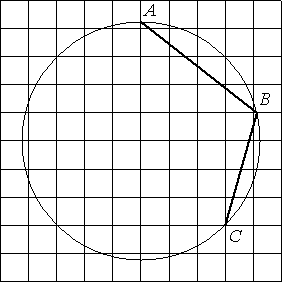Найдите угол ABC. Ответ дайте в градусах.
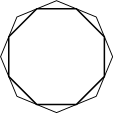Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: