
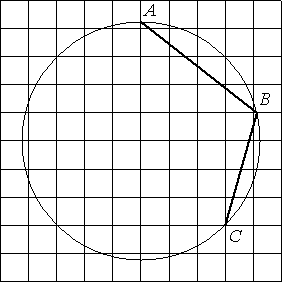
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
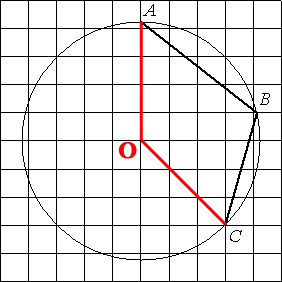 Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC равен 135° (прямой угол + половина от прямого угла, 90°+45°=135°).
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается (ABC), тоже равна 135°.
Следовательно, бОльшая дуга имеет градусную меру 360°-135°=225°
∠ABC -
вписанный угол, опирается на бОльшую дугу и по
теореме равен 225°/2=112,5°
Ответ: 112,5
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
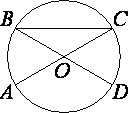 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
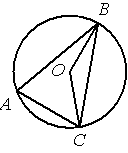 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Комментарии: