
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
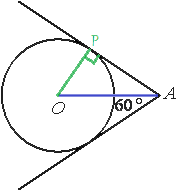 Проведем отрезок АО.
Проведем отрезок АО.
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является радиусом и перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР.
Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР.
АО является биссектрисой угла, образованного касательными (свойство касательных прямых). Следовательно, угол РАО равен половине данного угла, т.е. 30°.
sinPAO=OP/AO (по определению синуса).
sin30°=8/AO
1/2=8/AO (по таблице синусов)
1=2*8/AO
AO=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 3√
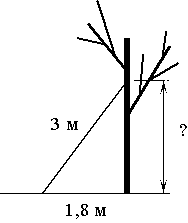 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Косинус острого угла A треугольника ABC равен 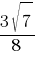 . Найдите sinA.
. Найдите sinA.
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Комментарии:
(2019-01-26 16:56:06) Администратор: Данила, я расписал решение немного подробней, надеюсь, стало понятней. Если нет, пишите.
(2019-01-25 16:13:14) Данила: И почему мы взяли именно значение синуса?
(2019-01-25 15:51:47) Данила: Откуда взято 2?
(2016-12-05 22:33:33) Администратор: катя, посмотрите задачу 101 из раздела "Статистика и теория вероятностей", очень похожа на Вашу.
(2016-12-05 17:26:10) катя: В среднем на 50 карманных фонариков, поступивших в продажу, приходится восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен