
 В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=8/0,4=20.
Ответ: AB=20.
Поделитесь решением
Присоединяйтесь к нам...
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=40.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=40.
 Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
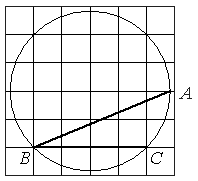 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
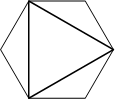 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Комментарии:
(2015-05-24 17:31:23) Администратор: Григорий, спасибо. Исправлено.
(2015-05-24 13:41:59) Григорий: в решении допущена ошибка при делении 8 на 0,4 получается 20, а не 5