Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
По свойству
равнобедренной трапеции - углы при основании равны. Тогда /ABC=/BCD=25°+100°=125°.
Сумма углов четырехугольника равна 360°, тогда получаем, что 360° = 125° + 125° + /BAD + /ADC,
/BAD+/ADC=360°-125°-125°=110°, а учитывая, что /BAD=/ADC (по тому же
свойству равнобедренной трапеции), получаем /BAD=/ADC=110°/2=55°, эти углы и есть меньшие в трапеции
Ответ: меньший угол трапеции = 55°.
Поделитесь решением
Присоединяйтесь к нам...
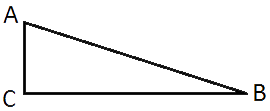Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
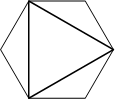Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
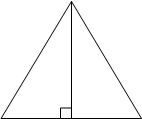Высота равностороннего треугольника равна
15√
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-24 18:26:39) Администратор: Аида, Вы забыли еще про два угла, посмотрите повнимательней.
(2015-05-24 17:11:43) Аида: 125+125= 250 же будет,почему вы 360 написали?