
 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
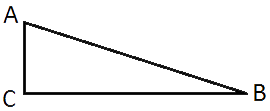
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
AB=85, AC=40
По
теореме Пифагора найдем второй катет:
AB2=AC2+BC2
852=402+BC2
BC2=7225-1600
BC2=5625
BC=75
Площадь любого треугольника равна половине произведения
высоты и стороны, к которой проведена
высота. В
прямоугольном треугольнике
высота совпадает с одним из катетов, получается, что площадь
прямоугольного треугольника равна половине произведения катетов.
SABC=(AC*BC)/2=(40*75)/2=1500
Ответ: 1500
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
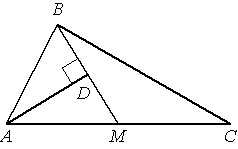 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
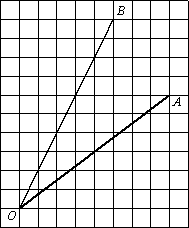 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Комментарии:
(2020-12-22 17:10:53) арсен: Найти неизвестный катет прямоугольного треугольника, если его гипотенуза равна 85 см, а один из катетов 13 см.