
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
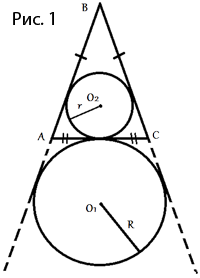 Проведем следующие отрезки (как показано на рисунке 2):
Проведем следующие отрезки (как показано на рисунке 2):
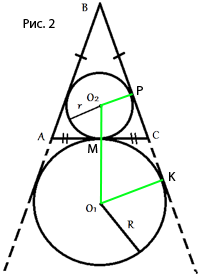 1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
2) Из точки О1 к точке касания окружности и продолжения стороны ВС. (Точка К)
3) Из точки О1 к точке О2.
Заметим, что:
1) СМ=АС/2.
2) СР=СМ, по
второму свойству касательной.
3) СМ=СК, по
второму свойству касательной.
4) O1O2=R+r.
5) O2Р перпендикулярна BC, по
первому свойству касательной.
6) O1К тоже перпендикулярна BC, по
свойству касательной.
7) Из пунктов 2) и 3) следует, что СР=СК=СМ=АС/2. Тогда РК=АС/2+АС/2=АС.
Следовательно, O2Р ||
O1К (по
свойству параллельных прямых). Отсюда следует, что
О1О2РК - прямоугольная трапеция (по
определению трапеции).
Рассмотрим эту трапецию.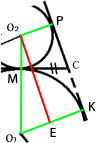
Проведем отрезок О2Е параллельный РК, а раз он параллелен РК, то в свою очередь перпендикулярен О1К и равен ему. Следовательно получившийся треугольник O1O2Е -
прямоугольный.
Тогда, по
теореме Пифагора, мы можем записать: (O1O2)2=(O2Е)2+(O1Е)2.
Подставим известные нам данные, полученные ранее:
(R+r)2=AC2+(R-r)2. Раскрываем скобки, получаем:
R2+2Rr+r2=AC2+R2-2Rr+r2
2Rr=AC2-2Rr
4Rr=AC2
r=(AC2)/4R
r=122/4*8
r=144/4*8, r=4,5
Ответ: радиус вписанной окружности равен 4,5.
Поделитесь решением
Присоединяйтесь к нам...
 Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
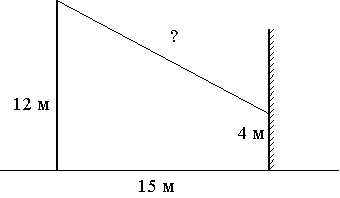 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
 В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Косинус острого угла A треугольника ABC равен 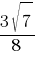 . Найдите sinA.
. Найдите sinA.
Комментарии:
(2024-05-15 17:53:09) Виолетта: В выпуклом четырехугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырехугольника NPQM можно описать окружность, PQ = 14, SQ = 4 .
(2016-09-01 13:14:52) Администратор: Александра, можно, рисунки добавлены.
(2016-08-22 15:56:46) Александра: А можно ли посмотреть рисунок к третьему свойству касатальной?
(2015-11-29 19:15:42) Администратор: Ксения, я не понял, а в чем разница между моим решением и Вашим?
(2015-11-24 00:13:26) Администратор: Ксения, я не понял, а в чем разница между моим решением и Вашим?
(2015-11-23 13:23:00) Ксения: А так правильно?: PC=CK=CM=6 Проведем О2Е - перпендикуляр к О1К. O2РКЕ-прямоугольник ,значит О2Е=РК=12 Тогда, по теореме Пифагора, мы можем записать: (O1O2)2=(O2Е)2+(O1Е)2.(R+r)2=144+(R-r)2. (R+r)2-(R-r)2=144. ((R+r)+(R-r))((R+r)-(R-r))=144 2R*2r=144 16 *2r=144 32r=144 r=4,5 .