
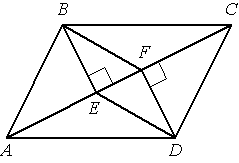
 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
1) Рассмотрим треугольники ABE и CDF.
AB=CD (по
свойству параллелограмма).
/BAE=/DCF (т.к. это
внутренние накрест-лежащие углы для параллельных BC и AD и секущей AC).
/BEA=/DFC (т.к. оба эти угла прямые по условию).
Если два угла у данных треугольников попарно равны, то и третьи углы равны (по
теореме о сумме углов треугольника).
Следовательно треугольники ABE и CDF равны (по
второму признаку равенства треугольников). Отсюда следует, что BE=FD
2) Рассмотрим треугольники BFE и DEF.
BE=FD (из пункта 1), EF-общая сторона, /BEF=/DFE (т.к. это прямые углы по условию).
Следовательно треугольники BFE и DEF равны (по
второму признаку равенства треугольников). Отсюда следует, что BF=ED.
Поделитесь решением
Присоединяйтесь к нам...
 Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
 В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
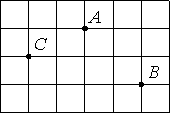 На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Комментарии: