Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
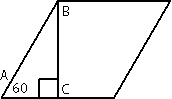Рассмотрим треугольник АВС.
Этот треугольник
прямоугольный (по условию задачи).
∠С=90°, так как это прямой угол.
∠A=60°, следовательно по
теореме о сумме углов треугольника:
180° = ∠АВС + ∠А + ∠С
180° = ∠АВС + 60° + 90°
∠АВС = 180°-90°-60°=30°.
По
свойству прямоугольного треугольника:
АС=АВ/2=36/2=18.
Следовательно вторая половина стороны ромба = 36-18=18.
Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 18 и 18.
Поделитесь решением
Присоединяйтесь к нам...
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
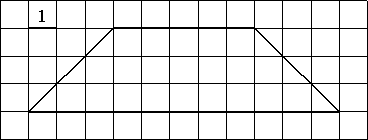Найдите площадь трапеции, изображённой на рисунке.
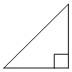В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
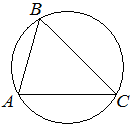В треугольнике ABC угол C равен 45°, AB=6√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-11-26 20:34:53) Администратор: марк, я внес уточнения в решение задачи, так понятней?
(2016-11-25 20:25:34) марк : откуда взялось 90 ° ?
(2015-04-19 11:27:53) Администратор: Алина, АВ - это сторона ромба, а по условию она равна 36.
(2015-04-19 09:54:27) Алина: Почему АВ стало равным 36?