
 Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
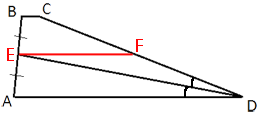 Проведем отрезок, параллельный основаниям, как показано на рисунке.
Проведем отрезок, параллельный основаниям, как показано на рисунке.
EF -
средняя линия трапеции, так как соединяет середины боковых сторон трапеции (по
теореме Фалеса).
∠ADE=∠DEF (так как это
накрест-лежащие углы при параллельных прямых EF и AD и секущей ED).
Получается, что ∠DEF=∠EDF (так как DE -
биссектриса).
Значит треугольник EFD -
равнобедренный (по
свойству равнобедренного треугольника).
Следовательно, EF=FD (по
определению).
EF=FD=CD/2=25/2=12,5
EF=(BC+AD)/2=12,5
(5+AD)/2=12,5
5+AD=25
AD=20
Дальше площадь трапеции можно найти разными способами:
1) Вычислить
высоту трапеции. И вычислить площадь через высоту
2) Вычислить площадь через стороны трапеции.
Первый вариант
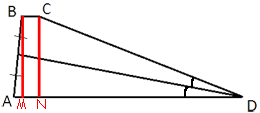 Проведем
высоты как показано на рисунке.
Проведем
высоты как показано на рисунке.
MN=BC=5 (т.к. BCNM -
прямоугольник).
BM=CN=h
Обозначим AM как x, для удобства.
AD=AM+MN+ND
20=x+5+ND
ND=15-x
Для треугольника ABM запишем
теорему Пифагора:
AB2=h2+x2
202=h2+x2
h2=400-x2
Для треугольника CDN запишем
теорему Пифагора:
CD2=h2+ND2
252=h2+(15-x)2
625=h2+(15-x)2
Подставляем вместо h2 значение из первого уравнения:
625=400-x2+(15-x)2
625-400=-x2+152-2*15*x-x2
225=152-2*15*x
225=225-30x
30x=0
x=0, получается, что BM совпадает со стороной AB, т.е. AB является высотой трапеции.
Тогда площадь трапеции равна:
S=AB(AD+BC)/2=20(20+5)/2=10*25=250
Второй вариант
Площадь трапеции можно найти по
формуле.
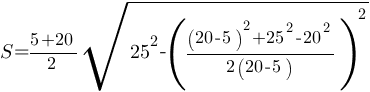
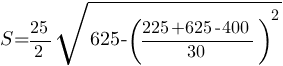
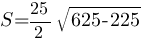
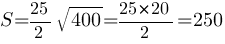
Ответ: 250
Поделитесь решением
Присоединяйтесь к нам...
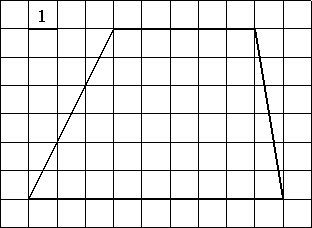 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Косинус острого угла A треугольника ABC равен 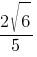 . Найдите sinA.
. Найдите sinA.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
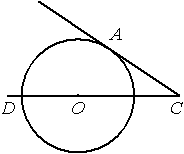 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
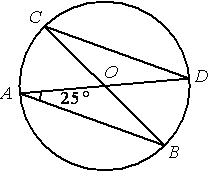 В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
Комментарии:
(2015-05-25 14:33:55) : Всеволод вообщето мы в школе изучаем формулу герона... Верните решение с формулой герона
(2015-03-16 15:09:26) Администратор: Всеволод, спасибо Вам за участие!
(2015-03-16 12:06:14) Всеволод: Спасибо за отклик! Теперь решение простое и точно в рамках программы, без волшебного "заметим" и без формулы Герона, наличие которой в программе тоже надо уточнять.
(2015-03-15 22:34:37) Администратор: Всеволод, я воспользовался Вашим советом и добавил решение без сложной формулы. Немного не так как писали Вы, но идея так же. Спасибо за подсказку!
(2015-03-12 12:41:42) Всеволод: Были глюки ... Пожалуйста, удалите дубликат сообщения и исправьте "с прямым углом в вершине C" на "с прямым углом в вершине H". Извиняюсь.
(2015-03-12 12:35:06) Всеволод: Применение такой формулы площади трапеции как-то не очень вписывается в программу. Проведём CH||BA и рассмотрим треугольник CDH. У него CD=25, DH=(DA-BC)=15, CH=AB=20. Заметим(!), что 25^2=15^2+20^2, т.е. треугольник CDH прямоугольный с прямым углом в вершине С. Значит CH=AB=20 является высотой трапеции, откуда сразу площадь трапеции 20х12.5=250. Если не заметили, что треугольник CDH прямоугольный, то дважды ищем его площадь: по формуле Герона (она ближе к программе) и как половина произведения основания DH на высоту, откуда находим нужную нам высоту и потом площадь трапеции.