
Косинус острого угла A треугольника ABC равен 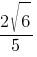 . Найдите sinA.
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
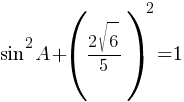
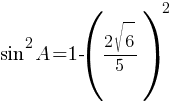
По правилам действий со степенями:
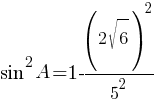
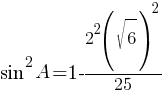
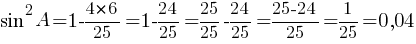
sinA=√0,04=0,2
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
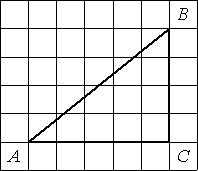 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
 В треугольнике ABC угол C равен 90°, BC=5, AC=2.
В треугольнике ABC угол C равен 90°, BC=5, AC=2.
Найдите tgB.
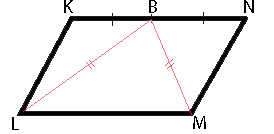 В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Комментарии: