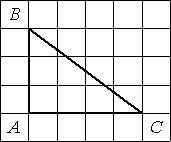
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

Другие задачи из этого раздела

Задача №0F5583

Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.

Задача №90F613

Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.

Задача №EA83A7

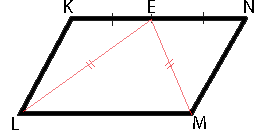В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.

Задача №DBC925

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.

Задача №06177F

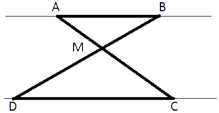Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.