
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
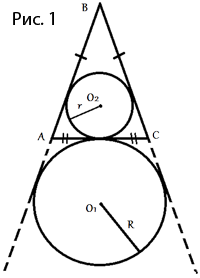 Проведем следующие отрезки (как показано на рисунке 2):
Проведем следующие отрезки (как показано на рисунке 2):
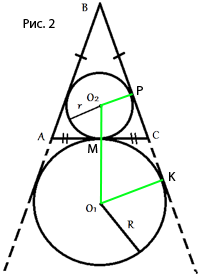 1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
2) Из точки О1 к точке касания окружности и продолжения стороны ВС. (Точка К)
3) Из точки О1 к точке О2.
Заметим, что:
1) СМ=АС/2.
2) СР=СМ, по
второму свойству касательной.
3) СМ=СК, по
второму свойству касательной.
4) O1O2=R+r.
5) O2Р перпендикулярна BC, по
первому свойству касательной.
6) O1К тоже перпендикулярна BC, по
свойству касательной.
7) Из пунктов 2) и 3) следует, что СР=СК=СМ=АС/2. Тогда РК=АС/2+АС/2=АС.
Следовательно, O2Р ||
O1К (по
свойству параллельных прямых). Отсюда следует, что
О1О2РК - прямоугольная трапеция (по
определению трапеции).
Рассмотрим эту трапецию.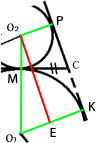
Проведем отрезок О2Е параллельный РК, а раз он параллелен РК, то в свою очередь перпендикулярен О1К и равен ему. Следовательно получившийся треугольник O1O2Е -
прямоугольный.
Тогда, по
теореме Пифагора, мы можем записать: (O1O2)2=(O2Е)2+(O1Е)2.
Подставим известные нам данные, полученные ранее:
(R+r)2=AC2+(R-r)2. Раскрываем скобки, получаем:
R2+2Rr+r2=AC2+R2-2Rr+r2
2Rr=AC2-2Rr
4Rr=AC2
r=(AC2)/4R
r=62/4*4,5
r=36/4*4,5, r=2
Ответ: радиус вписанной окружности равен 2.
Поделитесь решением
Присоединяйтесь к нам...
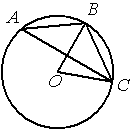 Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
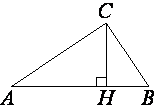 В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
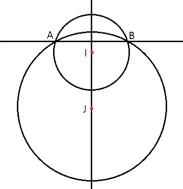 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
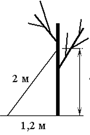 Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Комментарии:
(2016-10-31 17:57:39) Алина: Здравствуйте, скажите, пожалуйста, можно ли как-нибудь открыть просто правила?
(2015-05-26 20:11:08) Verbizhkiy rulit :***: Администратор, вы сделали такую здоровскую работу))) Спасибо вам от всех учеников лицея 265 и от меня лично)) У вас отличный сайт и, я уверенна, отличная команда))) Завтра экзамен и я благодаря вам буду стараться повысить свою оценку:3 Спасииибоооо
(2015-05-26 14:56:09) Юлия: боооожечки...-_-
(2015-05-25 16:30:41) Администратор: Татьяна, O11E=O1K-EK, O1K - это R, EK=O2P=r
(2015-05-25 13:30:02) Татьяна: Почему O1Е = R-r?
(2015-03-30 14:56:23) Айгуль: Спасибо Вам огромноеее)))
(2015-03-22 14:05:07) Софья: Обалдеть.