
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
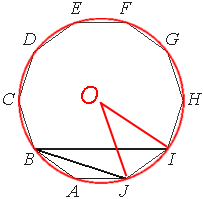 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам десятиугольника образуют равные углы, так как разбивают десятиугольник на равные треугольники.
Такой угол (например ∠IOJ) равен 360°/10=36°
∠IOJ является
центральным, следовательно градусная мера дуги тоже равна 36°
∠IBJ тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠IBJ=36°/2=18° (по
теореме о вписанном угле)
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
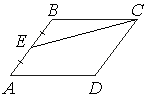 Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
Комментарии: