Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Рассмотрим каждое утверждение.
1) "Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники
подобны", это утверждение верно по
признаку подобия треугольников.
2) "Смежные углы равны", это утверждение неверно. По
определению, сумма смежных углов равна 180°, поэтому они будут равны только в одном случае, когда равны 90 градусам. В остальных случаях, смежные углы не равны.
3) "Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой", это утверждение верно. Это
свойство равнобедренного треугольника.
Поделитесь решением
Присоединяйтесь к нам...
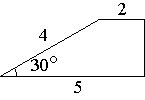Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
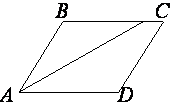Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
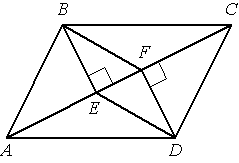В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: