
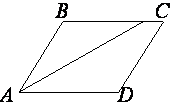 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
 ∠BCA=∠DAC=1° (т.к. это
накрест-лежащие углы)
∠BCA=∠DAC=1° (т.к. это
накрест-лежащие углы)
А так как AC -
биссектриса, то ∠BAC=∠DAC=1°.
∠A=∠BAC+∠DAC=1°+1°=2°
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
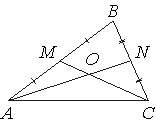 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Стороны AC, AB, BC треугольника ABC равны 2√
 Катеты прямоугольного треугольника равны 2√
Катеты прямоугольного треугольника равны 2√
 Высота равностороннего треугольника равна
15√
Высота равностороннего треугольника равна
15√
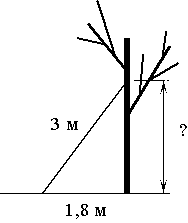 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Комментарии: