Катеты прямоугольного треугольника равны 2√
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=12+(2√
AB2=1+4*6=25
AB=5
Меньший угол лежит напротив меньшей стороны, 1<2√
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
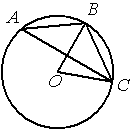Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Найдите площадь параллелограмма, изображённого на рисунке.
Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: