
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ619 –Η–Ζ 1087 |
 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è AD –Η BC ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 49 –Η 21, –Α ―¹―É–Φ–Φ–Α ―É–≥–Μ–Ψ–≤ –Ω―Ä–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Η AD ―Ä–Α–≤–Ϋ–Α 90¬Α. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η A –Η B –Η –Κ–Α―¹–Α―é―â–Β–Ι―¹―è –Ω―Ä―è–Φ–Ψ–Ι CD, –Β―¹–Μ–Η AB=20.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è AD –Η BC ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 49 –Η 21, –Α ―¹―É–Φ–Φ–Α ―É–≥–Μ–Ψ–≤ –Ω―Ä–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Η AD ―Ä–Α–≤–Ϋ–Α 90¬Α. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η A –Η B –Η –Κ–Α―¹–Α―é―â–Β–Ι―¹―è –Ω―Ä―è–Φ–Ψ–Ι CD, –Β―¹–Μ–Η AB=20.
–ü―Ä–Ψ–¥–Μ–Η–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD –¥–Ψ –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –¥―Ä―É–≥ ―¹ –¥―Ä―É–≥–Ψ–Φ.
 –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AED.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AED.
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ ―¹―É–Φ–Φ–Β ―É–≥–Μ–Ψ–≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α:
180¬Α=∠EDA+∠DAE+∠AED
180¬Α=90¬Α+∠AED
∠AED=90¬Α
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AED -
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η AED –Η BEC.
∠AED - –Ψ–±―â–Η–Ι
∠EBC=∠EAD (―².–Κ. ―ç―²–Ψ
―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ―΄–Β ―É–≥–Μ―΄)
–Δ―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η AED –Η BEC
–Ω–Ψ–¥–Ψ–±–Ϋ―΄ (–Ω–Ψ
–Ω–Β―Ä–≤–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤).
–Δ–Ψ–≥–¥–Α –Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Ω–Ψ–¥–Ψ–±–Η―è:
AD/BC=AE/BE
AD/BC=(AB+BE)/BE
49/21=(20+BE)/BE
49BE/21=20+BE
28BE/21=20
BE=20*21/28=15
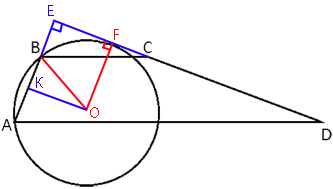 –û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ ―²–Ψ―΅–Κ―É F - ―²–Ψ―΅–Κ―É –Κ–Α―¹–Α–Ϋ–Η―è –Ω―Ä―è–Φ–Ψ–Ι CD –Η –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η.
–û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ ―²–Ψ―΅–Κ―É F - ―²–Ψ―΅–Κ―É –Κ–Α―¹–Α–Ϋ–Η―è –Ω―Ä―è–Φ–Ψ–Ι CD –Η –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η.
OF - –Η―¹–Κ–Ψ–Φ―΄–Ι ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η. –û–Ϋ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι EC (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –û–ö –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Ψ –ê–£.
OK - ―¹–Β―Ä–Β–¥–Η–Ϋ–Ϋ―΄–Ι –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä –Κ
―Ö–Ψ―Ä–¥–Β AB (
―²―Ä–Β―²―¨–Β ―¹–≤–Ψ–Ι―¹―²–≤–Ψ ―Ö–Ψ―Ä–¥―΄)
–ü–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ BK=AB/2=20/2=10.
EK=BE+BK=15+10=25
EK=OF=R=25, ―²–Α–Κ –Κ–Α–Κ OKEF - –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–û―²–≤–Β―²: 25
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AB=CD, ∠BDA=35¬Α –Η ∠BDC=58¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD AB=CD, ∠BDA=35¬Α –Η ∠BDC=58¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –≤–Β―Ä―à–Η–Ϋ―É C –Η –Κ–Α―¹–Α–Β―²―¹―è –Ω―Ä―è–Φ–Ψ–Ι AB –≤ ―²–Ψ―΅–Κ–Β B. –ù–Α–Ι–¥–Η―²–Β AC, –Β―¹–Μ–Η –¥–Η–Α–Φ–Β―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 8,4, –Α AB=4.
–û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –≤–Β―Ä―à–Η–Ϋ―É C –Η –Κ–Α―¹–Α–Β―²―¹―è –Ω―Ä―è–Φ–Ψ–Ι AB –≤ ―²–Ψ―΅–Κ–Β B. –ù–Α–Ι–¥–Η―²–Β AC, –Β―¹–Μ–Η –¥–Η–Α–Φ–Β―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 8,4, –Α AB=4.
 –£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–Η–Α–Φ–Β―²―Ä―΄ AD –Η BC, ―É–≥–Ψ–Μ
OAB ―Ä–Α–≤–Β–Ϋ 65¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α OCD.
–£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–Η–Α–Φ–Β―²―Ä―΄ AD –Η BC, ―É–≥–Ψ–Μ
OAB ―Ä–Α–≤–Β–Ϋ 65¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α OCD.
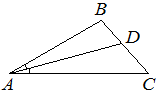 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ ∠BAC=28¬Α, AD βÄî –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ BAD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ ∠BAC=28¬Α, AD βÄî –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ BAD. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –Δ–Ψ―΅–Κ–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α, ―É–¥–Β―Ä–Ε–Η–≤–Α―é―â–Β–≥–Ψ ―³–Μ–Α–≥―à―²–Ψ–Κ –≤ –≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ–Ψ–Φ –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Η, –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 15 –Φ –Ψ―² –Ζ–Β–Φ–Μ–Η. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―³–Μ–Α–≥―à―²–Ψ–Κ–Α –¥–Ψ –Φ–Β―¹―²–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α –Ϋ–Α –Ζ–Β–Φ–Μ–Β ―Ä–Α–≤–Ϋ–Ψ 8 –Φ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―²―Ä–Ψ―¹–Α.
–Δ–Ψ―΅–Κ–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α, ―É–¥–Β―Ä–Ε–Η–≤–Α―é―â–Β–≥–Ψ ―³–Μ–Α–≥―à―²–Ψ–Κ –≤ –≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ–Ψ–Φ –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Η, –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 15 –Φ –Ψ―² –Ζ–Β–Φ–Μ–Η. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―³–Μ–Α–≥―à―²–Ψ–Κ–Α –¥–Ψ –Φ–Β―¹―²–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α –Ϋ–Α –Ζ–Β–Φ–Μ–Β ―Ä–Α–≤–Ϋ–Ψ 8 –Φ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―²―Ä–Ψ―¹–Α.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2018-01-19 21:22:57) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ï–≤–≥–Β–Ϋ–Η–Ι –ë–Α–Κ–Η–Ϋ, ―¹–Ψ–≥–Μ–Α―¹–Β–Ϋ ―¹ –£–Α–Φ–Η. –†–Β―à–Β–Ϋ–Η–Β ―É–Ω―Ä–Ψ―â–Β–Ϋ–Ψ –Ω–Ψ –£–Α―à–Β–Φ―É –≤–Α―Ä–Η–Α–Ϋ―²―É.
(2017-12-29 11:41:46) –ï–≤–≥–Β–Ϋ–Η–Ι –ë–Α–Κ–Η–Ϋ: –ü―Ä–Ψ―â–Β –Ϋ–Α–Ι―²–Η ―¹―Ä–Α–Ζ―É OF=EK=EB+BK=15+10=25