Известно, что a и b — положительные числа и a>b. Сравните 1/a и 1/b.
Посмотрим на поведение некоторого числа 1/x.
При стремлении х к бесконечности, дробь 1/х стремится к нулю. Иными словами: чем больше х, тем меньше 1/х - это называется обратная пропорциональность. Например: если x=10, то 1/х=0,1; а если х=100, то 1/х=0,01
Следовательно, если a>b, то (1/a)<(1/b).
Ответ: (1/a)<(1/b)
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение 1/x2+2/x-3=0.
В период распродажи магазин снижал цены дважды: в первый раз на 45%, во второй – на 20%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 700 р.?
Решите систему уравнений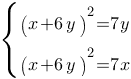 
Решение какого из данных неравенств изображено на рисунке?
1) x2-7x<0
2) x2-49>0
3) x2-7x>0
4) x2-49<0
Решите уравнение 2x2+14x=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: