
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны", это утверждение верно по
свойствам углов.
2)"В любой четырёхугольник можно вписать окружность", это утверждение неверно, т.к. должны выполниться
определенные условия.
3) "Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника", это утверждение верно, по
теореме об описанной окружности.
Поделитесь решением
Присоединяйтесь к нам...
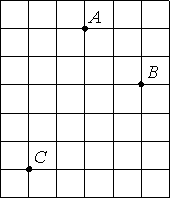 На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Косинус острого угла A треугольника ABC равен 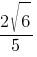 . Найдите sinA.
. Найдите sinA.
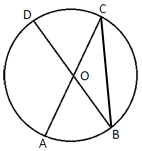 В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Комментарии: