Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
Рассмотрим каждое утверждение.
1) "Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны", это утверждение неверно, т.к. не соответствует ни одному из
признаков равенства треугольников.
2) "Площадь круга меньше квадрата длины его диаметра". Прощадь круга равна ΠR2, или ΠD2/4. Число Π (Пи) равно, приблизительно, 3,14. Тогда Sкруга=0,785D2. А это, конечно меньше, чем D2. Утверждение верно
3) "Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб", это утверждение неверно, т.к. полностью не соответствует ни одному
свойству ромба.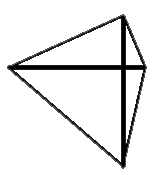
Например, четырехугольник, изображенный на рисунке, его диагонали перпендикулярны, но очевидно, что это не ромб.
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: