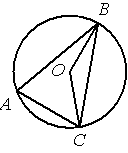Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=70°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 70°*2=140°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=140°.
Ответ: /BOC=140°.
Поделитесь решением
Присоединяйтесь к нам...
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Радиус вписанной в квадрат окружности равен 14√
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: