
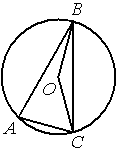
 Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=75°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 75°*2=150°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=150°.
Ответ: /BOC=150°.
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
3) Площадь круга меньше квадрата длины его диаметра.
 Найдите площадь ромба, если его диагонали равны 39 и 2.
Найдите площадь ромба, если его диагонали равны 39 и 2.
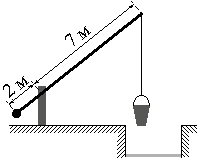 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Комментарии: