
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
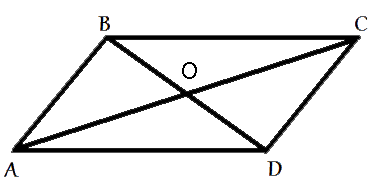 Рассмотрим треугольники ABC и ACD.
Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников, AB=CD и BC=AD (по
свойству параллелограмма), следовательно рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACD, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок DO - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь COD равна половине площади треугольника ACD. SCOD=SACD/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
 Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
 Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
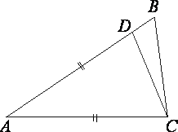 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
Комментарии: