
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Рассмотрим каждое утверждение.
1) "На плоскости существует единственная точка, равноудалённая от концов отрезка", это утверждение неверно, т.к. любая точка, принадлежащая
серединному перпендикуляру, равноудалена от концов отрезка (
свойство серединного перпендикуляра).
2) "Центром вписанной в треугольник окружности является точка пересечения его биссектрис", это утверждение верно (
свойство вписанной окружности).
3) "Если гипотенуза и острый угол одного
прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны". Прилежащий к известному острому углу катет равен проиведению косинуса этого угла на гипотенузу (из
определения косинуса). Следовательно этот катет тоже будет равен у обоих треугольников. Тогда по
первому признаку равенства, получается, что эти треугольники равны. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
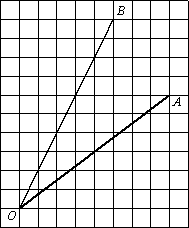 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
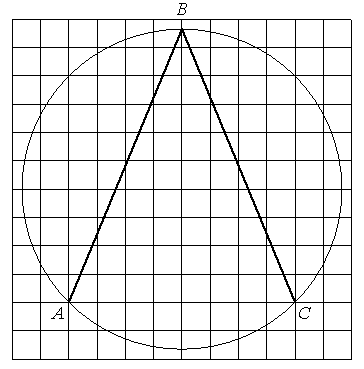 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
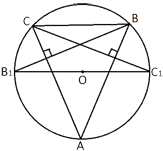 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
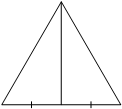 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Комментарии: