
 Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
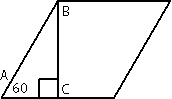 Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). ∠A=60°, следовательно по
теореме о сумме углов треугольника ∠АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=26/2=13. Следовательно вторая половина стороны ромба = 26-13=13. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). ∠A=60°, следовательно по
теореме о сумме углов треугольника ∠АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=26/2=13. Следовательно вторая половина стороны ромба = 26-13=13. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
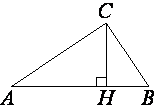 В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
Стороны AC, AB, BC треугольника ABC равны 2√
 В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
 Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Комментарии:
(2017-11-03 00:08:26) Администратор: Елена, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-10-23 22:02:17) елена: . Площадь ромба равна 18, а периметр равен 36. Найдите высоту ромба.