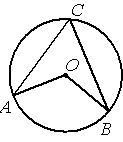
Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
По условию /AOB=130°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 130°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 130/2=65.
Ответ: /ACB=65°.
Поделитесь решением
Присоединяйтесь к нам...
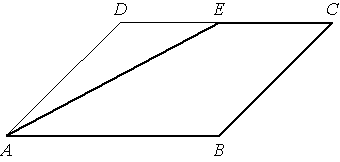Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь прямоугольного треугольника равна 578√
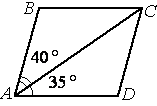Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
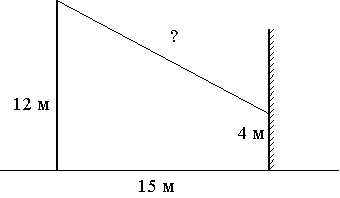От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
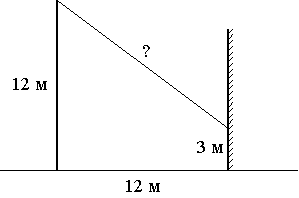От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: