
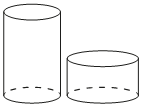
 Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
Объем цилиндра равен произведению основания на высоту:
Основание
цилиндра - круг, его площадь равна:
S=πR2
Число π приблизительно равно 3.14, но не будем его подставлять, так как в итоге оно сократится и ответ будет более точен:
S1=π62=36π
S2=π92=81π
V1=S1*h1=36π*9=324π
V2=S2*h2=81π*2=162π
V1/V2=324π/162π=2
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
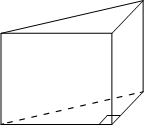 В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
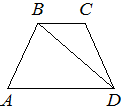 В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
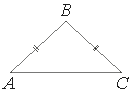 В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
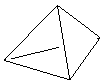 Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
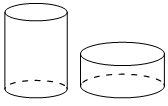 Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
Комментарии: